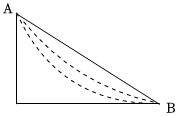
在只考慮重力的作用的情況下，不計摩擦力，一小球在豎直面從A點沿某條曲線下滑到B點，問怎樣的曲線能使所走的時間最短？這一個問題被稱為最速降線問題（Brachistochrone），由約翰?伯努利在1696年提出來挑戰(zhàn)歐洲的數學家的，如圖，給你提供斜面可調整的光滑軌道和一個小球，請你設計實驗，證明最速降線是否真實存在？
（1）實驗器材：

秒表、斜面可調整的光滑軌道和小球

秒表、斜面可調整的光滑軌道和小球

；
（2）實驗步驟：

①把小球從直斜面的頂端自由釋放，記錄小球沿直斜面滑落到底端的時間t₁，
②改變斜面的彎曲程度，把小球從彎曲斜面的頂端自由釋放，記錄小球沿彎曲斜面滑落到底端的時間，
③再次改變斜面的彎曲程度，把小球從彎曲斜面的頂端自由釋放，記錄小球沿彎曲斜面滑落到底端的時間

①把小球從直斜面的頂端自由釋放，記錄小球沿直斜面滑落到底端的時間t₁，
②改變斜面的彎曲程度，把小球從彎曲斜面的頂端自由釋放，記錄小球沿彎曲斜面滑落到底端的時間，
③再次改變斜面的彎曲程度，把小球從彎曲斜面的頂端自由釋放，記錄小球沿彎曲斜面滑落到底端的時間

；
（3）實驗結論：

若t₁與后兩次實驗的時間相同，則最速降線不存在，若t₁與后兩次實驗的時間不同，則最速降線存在

若t₁與后兩次實驗的時間相同，則最速降線不存在，若t₁與后兩次實驗的時間不同，則最速降線存在

。（開放性試題，答案合理即可）